This study aims to evaluate the effectiveness of vaccination in curbing the spread of emerging SARS-CoV-2 variants using the SEVIAR mathematical model with Caputo fractional orders. The model integrates vaccine-induced immunity and assesses the impact of vaccination on transmission dynamics while determining herd immunity thresholds.
MethodThe SEVIAR model was applied to real-world data from Rivers State, Nigeria, to simulate disease transmission dynamics within vaccinated populations. Fractional calculus was employed to address the complexities of disease spread and the nuanced effects of vaccination. Sensitivity analyses and computer simulations were performed to examine the influence of varying vaccination rates and timing on mitigating variant transmission and reducing hospitalization rates.
ResultsThe findings demonstrate a strong association between higher vaccination rates and decreased transmission and hospitalization, even amid the emergence of new SARS-CoV-2 variants. Sensitivity analysis highlighted the critical role of early diagnosis and timely immunization in controlling the spread of variants. Thresholds for achieving herd immunity were identified, underscoring the need for sustained high vaccination coverage to manage variant transmission effectively.
ConclusionsThe study underscores the importance of continuous and robust vaccination campaigns, particularly in the context of evolving COVID-19 variants. It highlights the utility of fractional calculus in modeling the dynamics of SARS-CoV-2 variants and optimizing public health responses. For policymakers, these findings provide valuable guidance in formulating strategies to address the challenges posed by emerging virus strains. Given the virus's evolving nature, ongoing evaluation of vaccine efficacy and adaptive public health strategies are essential to controlling the pandemic effectively.
El objetivo de este estudio es evaluar la efectividad de la vacunación, para frenar la propagación de las variantes emergentes de SARS-CoV-2 utilizando el modelo matemático SEVIAR con órdenes fraccionales de Caputo. Dicho modelo integra la inmunidad inducida por la vacuna y evalúa el impacto de la vacunación en la dinámica de la transmisión, a la vez que determina los umbrales de la inmunidad de grupo.
MétodoSe aplicó el modelo SEVIAR a los datos del mundo real del Estado de Rivers, Nigeria, para simular la dinámica de la transmisión de la enfermedad dentro de las poblaciones vacunadas. Se utilizó el cálculo fraccional para abordar las complejidades de la propagación de la enfermedad y los efectos matizados de la vacunación. Se realizaron análisis de sensibilidad y simulaciones informáticas para examinar la influencia de las tasas de vacunación variables y el tiempo en la mitigación de la transmisión de las variantes y la reducción de las tasas de hospitalización.
ResultadosLos hallazgos demuestran una fuerte asociación entre las tasas de vacunación más elevadas y la reducción de la transmisión y hospitalización, incluso en mitad de la emergencia de las nuevas variantes de SARS-CoV-2. El análisis de sensibilidad destacó el papel esencial del diagnóstico temprano y la inmunización oportuna para controlar la propagación de las variantes. Se identificaron los umbrales para alcanzar la inmunidad de grupo, subrayando la necesidad de una cobertura de vacunación sostenida para manejar la transmisión de la variante efectivamente.
ConclusionesEl estudio destaca la importancia de las campañas de vacunación continuas y sólidas, particularmente en el contexto de las variantes de COVID-19 en evolución. Destaca la utilidad del cálculo fraccional para modelar la dinámica de las variantes de SARS-CoV-2 y optimizar las respuestas de la sanidad pública. Para las autoridades responsables, estos hallazgos proporcionan una guía valiosa para la formulación de estrategias que aborden las dificultades que plantean las cepas de virus emergentes. Dada la naturaleza evolutiva de los virus, la evaluación continua de la eficacia de la vacuna y las estrategias de salud pública adaptativas son esenciales para controlar la pandemia de manera efectiva.
COVID-19 is still changing as of December 2024, with new strains appearing and impacting public health reactions, symptomatology, and transmission rates. New SARS-CoV-2 mutations have been discovered in recent months. Notably, the XEC variant has been identified and is being monitored for possible effects on vaccination effectiveness and transmission. The symptoms of COVID-19 are still varied and can range from minor to severe. Fever, coughing, dyspnea, sore throat, loss of taste or smell, and exhaustion are typical symptoms. It's crucial to remember that even those who have had vaccinations may have symptoms, albeit they are usually less severe. Testing is necessary for an appropriate diagnosis because of the overlap with other respiratory disorders. The mainstay of the fight against COVID-19 is still vaccination. In order to improve effectiveness against new viral types, recent advancements have included the development of novel mRNA vaccines that target certain virus components. Australian scientists, for example, have created a possible mRNA vaccine that addresses immune imprinting problems and may provide improved protection against variations such as Omicron. Health officials continue to advice immunization, hand washing, wearing masks in crowded or dangerous situations, and remaining at home when exhibiting symptoms as preventive measures. In order to prevent transmission and safeguard susceptible groups, these tactics are essential.1–4 The Omicron strain is a new and developing threat that has many unknowns about its transmission dynamics and effects. This must be acknowledged. Sustained investigation and monitoring are required to comprehend this virus and develop efficient preventative measures.5 The Omicron variant's capacity to compromise immunological responses is also a major cause for concern. According to preliminary studies, the variation may be able to partially circumvent immunity acquired from previous infections and immunizations. The degree of immune evasion and how it affects hospitalization rates and the severity of diseases are yet unknown, though. Notwithstanding these ambiguities, there are still large gaps in our knowledge of the Omicron version. Public health interventions, including immunization, mask use, and social distancing, are still essential for reducing the symptoms associated with Omicron infections and stopping their spread.
A mathematical method used to analyze the Omicron variation is known as the Susceptible, Exposed, Infected, and Recovered (SEIR) model.6–10 By tracking an individual's travel between different compartments, this model separates people into four groups: susceptible, exposed, infected, and recovered. It does this by using differential equations. This allows us to determine the population in each compartment at any given time. It has been proposed that the Laplace transform method might be a workable solution for nonlinear biological processes since it may be utilized to solve both linear and nonlinear differential equations.
Since the Omicron variant is expected to be at least twice as transmissible as the previously common Delta strain, its high transmissibility is a serious cause for concern. As such, there is an increased danger of transmission from person to person, which could overwhelm healthcare facilities due to the sheer number of cases. Even in nations with high vaccination rates, the Delta variant increased in instances due to its higher contagiousness compared to previous versions; yet, there is still evidence indicating that it may also result in more severe illness.11,12 Nevertheless, additional research is required to confirm that the work's primary objective is to present the lemma and theorems needed to demonstrate the stability of the proposed fractional approximation scheme and the presence of a unique solution. This work describes a fractional modeling technique that uses the Caputo operator to study the dynamics of COVID-19. Numerous studies have employed this strategy to increase our understanding of virus transmission patterns. Researchers propose a novel method that uses a generalized Caputo-type non-integer-order derivative and a modified predictor–corrector scheme to investigate the nature of the disease. Moreover, mathematical models might be useful instruments for forecasting the Omicron variant's impact and dissemination. These models can help guide resource allocation decisions and public health policies, but they also need to be complemented by additional data sources and elements, like human behavioral characteristics and the efficacy of public health treatments.13 This strategy investigates the characteristics of fractional calculus integrals and derivatives of non-integer order,14 a branch of mathematics that is utilized in several of the publications cited in this research.15 Leibniz introduced fractional derivatives, also called semi-derivatives, in 1695, at the same time as fractional differential equations began to take shape.Scholars of fractional calculus investigate the properties of non-integer-order derivatives and integrals, as demonstrated by the range of applications examined in this work. For example,16,17 investigates a time-fractional model of HIV-I infection of CD4+ T cells and uses the fractional differential transform method to solve the corresponding fractional model.18 The Atangana-Baleanu derivative is also used to investigate whooping cough and phytoplankton feeding models. In light of the COVID-19 pandemic, drastic public health measures are needed to stop the spread of other variants like Omicron. In order to effectively monitor and respond to new variations, cooperation between governments and scientists globally is essential.19–21 Mathematical simulations and models are utilized in quantitative research to quantify the Omicron-type virus and then evaluate how well various countermeasures work by understanding the dynamics of its transmission. In addition to considering the impact of population density and movement patterns, these studies also consider vaccination rates and the effectiveness of non-pharmaceutical therapies such as mask wear and self-isolation. Understanding and preventing the development of new variations such as Omicron requires the application of mathematical modeling22–28. Models that have been parameterized and validated with the help of real-world data7,13,29 help determine the effectiveness of interventions like immunization, therapy, and mask wearing. Moreover, research using fractional order models advances our knowledge.21,24,30–37 In particular, a versatile mathematical model that can be adjusted to different conditions is used to examine the dissemination of the Omicron variant.22,38,39 These models offer insights into the best control measures for reducing the virus's spread by taking into account variables like vaccination efficacy and rates of transmission.40 This study examines a mathematical model for hypertensive or diabetic COVID-19 patients using first-order nonlinear differential equations. The piecewise argument method reveals six equilibrium, including extinction and endemic states. Local stability and bifurcations are analyzed, showing chaos without quarantine. A hybrid control method manages bifurcations and chaos, highlighting quarantine's importance in COVID-19 control.41 In this research, first-order nonlinear differential equations are used to represent people with diabetes or hypertension who have been exposed to COVID-19. Six equilibria—extinction, boundary, quarantined-free, exposure-free, endemic, and susceptible-free—are identified after being discretized using the piecewise argument approach. Analysis of stability, bifurcations, and chaos reveals instability in the absence of quarantine. To quell chaos, a hybrid control approach is suggested, highlighting the function of quarantine in COVID-19 management.42
In this research, first-order nonlinear differential equations are used to represent people with diabetes or hypertension who have been exposed to COVID-19. Six equilibria—extinction, boundary, quarantined-free, exposure-free, endemic, and susceptible-free—are identified after being discretized using the piecewise argument approach. Analysis of stability, bifurcations, and chaos reveals instability in the absence of quarantine. To quell chaos, a hybrid control approach is suggested, highlighting the function of quarantine in COVID-19 management.43 Originating in Wuhan, China, this study examines the dynamics of COVID-19 using a fractional epidemic model. The impact of quarantine and latent periods on infection rates is investigated using a transmission model. The model is numerically solved using data from Maharashtra, India, using the Laguerre collocation approach (15th–21st April 2020). Parameter differences for upper and lower bounds are shown graphically for fractional and integer-order solutions.44 The severity of COVID-19's global spread has varied. In order to forecast the size and duration of the epidemic, this study examines its transmission dynamics. Cases increased from January 30, 2020, when it was discovered in India, to April 21, 2020. A fractional model utilizing Genocchi collocation and Caputo-Fabrizio derivatives was analyzed using data collected between April 15 and April 21, 2020. In order to stop the spread, the results highlight the importance of lockdowns, social distancing, and self-quarantine.45 To examine COVID-19 dynamics, fractional-order models that take memory and genetic influences into account have been employed (Moira & Xu, 2003). These models evaluate virus distribution successfully, and they include modified SIR and SEIR variations. Using the Atangana-Baleanu derivative, this work proposes a nonlinear fractional-order model that includes a vaccination group and two quarantine classes. They construct a threshold parameter for the model by employing fixed point theorems to demonstrate the existence and uniqueness of solutions.46 Recent SARS-CoV-2 XBB and BQ subvariants show enhanced resistance to neutralizing antibodies, even in vaccinated individuals or those with prior Omicron infections. This study develops a mathematical model accounting for immunity against new variants, particularly Omicron. Stability and equilibrium analysis are conducted, with numerical simulations showing control strategies reduce COVID-19 spread.47 Vaccines have been developed in response to the global spread of the coronavirus since December 2019. Distribution efficiency is still a major problem. Using a Susceptible-Exposed-Infectious-Recovered (SEIR) model with vaccine components, this paper simulates vaccination techniques through the use of mathematical modeling and reinforcement learning. Numerical simulations demonstrate the effectiveness of the four strategies that are developed.48 In this work, a fractional-order fuzzy dynamical system that models the COVID-19 pandemic is examined. Using fixed point theory, the model's uniqueness and accuracy are examined. Iterative techniques using the Caputo and Attangana-Baleanu fractional derivatives are used to generate numerical solutions. In order to demonstrate the approach and account for uncertainty, a random COVID-19 model utilizing random differential equations is also provided, along with numerical approximations.48 This article investigates the transmission dynamics of COVID-19 using the SEIR model with two non-singular kernel fractional derivative operators, the Caputo–Fabrizio (CF) and Atangana–Baleanu (ABC) models, which were used to assess memory effects and forecast long-term disease trajectories. The basic reproduction number and equilibrium point stability were analyzed, and the existence and uniqueness of solutions were investigated. The comparison showed that the ABC approach significantly affected epidemic dynamics for non-integer τ values, whereas the CF approach was appropriate for mild cases, and both approaches produced the same results for integer τ values. To successfully manage and limit the spread of COVID-19 and its variations, interdisciplinary research combining mathematical modeling, epidemiology, and public health interventions is necessary. This work is unique in that it studies the dynamics of the Omicron variant in Rivers State, Nigeria, using actual NCDC data, as opposed to previous research, which frequently used simulated or national-level data. It includes vaccination efficacy in a Caputo fractional order model, resulting in a more detailed understanding of transmission dynamics. The use of the Laplace-Adomian Decomposition Method (LADM) and a detailed sensitivity analysis improves the investigation of many factors impacting infection transmission. The findings have important implications for creating targeted public health initiatives to effectively restrict the spread of the Omicron variant. This study's novelty lies in its innovative approach to simulating the transmission dynamics of SARS-CoV-2 variants and assessing the effectiveness of vaccination. It introduces a novel SEVIAR model with Caputo fractional orders to evaluate the impact of vaccination in controlling SARS-CoV-2 variants, providing an accurate representation of transmission dynamics by incorporating memory and hereditary effects. The model underscores the importance of early and frequent vaccinations in reducing transmission and hospitalization, even as variants emerge, and identifies critical herd immunity thresholds. Using real-world data from the Nigeria Centre for Disease Control (NCDC) for Rivers State, sensitivity analysis and fractional calculus demonstrate the crucial role of early vaccination and high vaccination rates in curbing the spread of variants and lowering hospitalization rates. This enhances our understanding of how timing influences public health outcomes.
PreliminaryDefinition 1 [8]. Ωχ,χ>0,in space Cμ,μ∈R iff m>μ: Ωχ=χmΩ1χ. where Ω1χ∈C0∞,∀Ωn∈Cμ,n∈N. then. Order of fractional integration Ψ≥0 for function Ωχ∈Cμ,μ≥−1χ>0: AlsoDΨΩχ=1ΓΨ∫0tχ−tΨ−1Ωχdχ. Such that DΨΩχ=Ωχ. said to be Riemann-Liouville fractional integration [8]. Function ξt,t≥0. Then Laplace transform ξs=∫0∞ξte−stdt.
ξt using order Ψ is defined as LΩΨt=ϑΨLΩt−ϑΨ−1Ω0−ϑΨ−2Ω′0−ϑΨ−3Ω′′0⋯.
fΩss⇒L−1Ωss=∫0tΩtdt.Definition 3 [8] Z0,Z1,.…Zn stands for the Adomian polynomials is comprised of breaking down the function to be determined bt into a series of the kind.
bt=b0+b1+b2+⋯bn as could be stated:
Uniqueness of solution's and existenceTheorem 1 [8]: Let
Consider Q as a region in (i + 1)-dimensional space, with one dimension corresponding to t and the other i dimensions corresponding to the vector f{x} if the partial derivative dfdxi=1,2,3.…… continuously distributed within.
Q={at:\a−a0\≤b,\t−t0≤x then there δ≥0.
And exist a unique x=a1ta2ta3tant interval t−t0\≤δ.
MethodsClassical order model formulation descriptions variantIn this section, we examine a mathematical model designed to explain the intricate dynamics of viral variants. By incorporating factors such as transmission rates and immunization effectiveness, the model provides a comprehensive view of the transmission dynamics of SARS-CoV-2 variants. It distinguishes between susceptible, vaccinated, symptomatic, and recovered individuals, highlighting their roles in the spread of the virus.
The modified modelThe set of equations now includes the Caputo fractional order derivative, which improves the mathematical model. This improvement allows the memory effect to be studied using fractional-order derivatives. The system of ordinary differential equations has been modified as a result, as explained below.
1Γα+1∫t0tt−sα−2dt To accommodate temporal variance, we include a process kernel spanning the interval [t, t_0]. By applying the fractional derivatives of order α+1 to both sides of eq. (1), we build a fractional order model using generalized time-dependent decomposition, where these fractional derivatives serve as the left inverse of fractional integrals. As a result, we receive:
And descriptions of the various variables in the model are presented in table 1 below.
Varaible and Parameter,
| St | Individual at risk throughout time. |
| Vt | Vaccinated individual over time. |
| Et | Somebody who has been exposed over time. |
| It | Over time, an infected person. |
| At | Individual antiviral medication over time. |
| Rt | Over time, the patient recovered. |
| β | ΛRecruitment rate. |
| ε | Rate of vaccination. |
| β | Transmission rate. |
| θ | Rate of recovery from infectious. |
| ωψ | Proportion of infected individual receiving antiviral treatment. |
| φ | Rate of waning immunity due to vaccination. |
| ρ | The proportion rate in which people complete antiviral treatment. |
| μ | The natural mortality rate among all individuals. |
| σ | Death induced by the disease. |
| τ | The rate at which individuals progress from being exposed to becoming infected. |
Theorem 1 [8].
Let:
By taking a partial derivative, the following solution is obtained, which is singular in nature according to the model;
Also, obtaining the second function's partial derivative i.e.
g2=JtαVt=σ−φ−μVt. To achieve this:
The third function's partial derivative may be obtained in a similar manner. i.e.
To achieve this;
Fourth function's partial derivative may be obtained in a similar manner.
g4=JtαIt=τEt−μ+θIt−ωAtIt. To achieve this;
The fifth function's partial derivative may be obtained in a similar manner. i.e.
g5=JtαAt=ωAtIt−ρ+μA. To achieve this;
The sixth function's partial derivative may be obtained in a similar manner. i.e.
The existence of a partial derivative confirms that it is both mathematically and biologically valid, as demonstrated by Theorem 1, as it is both continuous and bounded. Moreover, the problem possesses a unique solution.
Evaluation of states of stabilityEquilibrium without disease
Eq. (8)’s right side can be set to zero to determine the equilibrium point. The following equations can be resolved after the disease-related classes E, I, and A are substituted with zero:
The disease equilibrium is reached at critical points as;
Equilibrium state in an endemic condition
When a disease continues to spread throughout a community, it reaches endemism equilibrium, also known as a non-zero equilibrium condition. In the endemic equilibrium state, the values are non-zero, indicating the continued presence of the disease, in contrast to the disease-free state, where E = I = A = R = 0.
Fundamental reproduction numberThe SVEIAR model's Fundamental Reproduction Number and disease rate of regeneration are both correlated. If the system reaches this equilibrium's threshold R0<1, the disease will disappear, and an epidemic will begin.
Analysis of sensitivity regarding the fundamental reproduction number
The sensitivity study determines the main factors influencing the reproductive number of the Omicron variant and looks at how the model reacts to changes in parameters.
In population simulation, this guides parameter manipulation by measuring state variable changes through parameter changes. According to the definition displayed in According to Fig. 1, a variable n that is differentiable from a parameter k has the following normalized forward sensitivity index:
Utilize the Laplace-Adomian decomposition methodBy applying Laplace Adomian Decomposition method on (8).
where Jtα0≤α≤1 is the Non-integer fractional order, α demonstrate the fractional time order, we perform a Laplace transform in eq. (10), resulting in the following:
Initial condition
Laplace's transform definition gives us.
Simplify (14)
We derive the equation from the initial condition (16)
Considering that the technique provides an infinite series solution,
The nonlinear term involved are ItSt, VtSt, ItAt can be expressed as
Where Xn,Yn,Zn signifies Adomain polynomials provided by
Substitute eqs. (17), (18) and (19) into (16), we get
We apply the term in eq. (20) repeatedly and then use Laplace inversion to get the solution for every compartment, which gives us the whole model formula.
The followings were obtained from (21)(21);
When n = 0, from first equation of (21)
In eq. (21)‘s second equation, when n = 0, to obtain the following;
In eq. (21)‘s third equation, when n = 0, (21) to obtain this;
In eq. (21)‘s fourth equation, when n = 0, (21) to obtain this;
In eq. (21)‘s fifth equation, when n = 0, (21) to obtain this;
In eq. (21)‘s sixth equation, when n = 0, (21) to obtain this;
In eq. (21)‘s first equation, when n = 1, (21) to obtain this;
In eq. (21)‘s second equation, when n = 1, (21) to obtain this;
In eq. (21)‘s third equation, when n = 1, (21) to obtain this;
In eq. (21)‘s fourth equation, when n = 1, (21) to obtain this;
In eq. (21)‘s fifth equation, when n = 1, (21) to obtain this;
In eq. (21)‘s sixth equation, when n = 0, (21) to obtain this;
ResultsUsing simulations of sensitivity index in the Table 2 below, we analyze and analyze how parameters affect and contribute to the basic reproduction numberℜ0. Λ Recruitment rate, τ rate of progression from exposed to infected, β the disease transmission show significant influence (Figs. 2, 5, 6). Notably, (Figs. 3, 4).are significantly affects the dynamics Omicron COVID-19 given in the Table 2 below.
We used real data from the NCDC of River State, Nigeria, and performed a numerical simulation in order to develop a better understanding of the dynamics and control of the Omicron variation of COVID-19. Based on the simulation's starting values and parameters, we assessed the outcomes as follows:
The following arbitrary order-series solution is obtained:
Taking the α=0.55,α=0.75,α=0.95,α=1.
Convergence
The contraction of the approximation solution to the precise solution is a necessary condition for the convergence of the approaches.
Theorem [8]: A mapping U:P→P is established for any on two Banach spaces.
p,p1∈P,//XP−XP1≤k//p−p1//,0 Using the Adomian decomposition method, the series in (15) can be expressed as follows: pm=Xpm−1,pm−1=∑pim=1,2,3,.…, and assume that pm∈Arp where Arp={p1∈P:ipm∈Arp;iilimn→∞pm=p. Proof. Fori, using mathematical induction for m=1, we have
Let the result is true for n=1, (then)
We have
pn−p=Xpn−1−Xp≤kpn−1−p≤knpn−p.(i.e)
(ii) pn−p≤knp0−p and as limn→∞kn=0, therefore, we have limn→∞pn−p=0⇒limn→∞pm=p.
DiscussionUtilizing the Laplace transformation and Adomian decomposition techniques allowed for an efficient investigation of the created model. The convergence analysis shows that the proposed technique consistently yields stable solutions across a range of parameter settings, thereby validating its dependability. The sensitivity chart in Fig. 1 illustrates how various parameters affect the basic reproduction number, R, highlighting factors essential to successful disease control measures. Specifically, it identifies the recruitment rate, the rate of progression from exposed to infected, and the disease transmission rate as the most significant contributors to R.
Figs. 2–6 demonstrate the parameter responses on R, showing how variations in individual parameters influence it. An increase in either the recruitment rate or the disease transmission rate leads to a rise in R, which reflects the spread of the disease. The dynamics of R0R_0R0 are also influenced by the rate of progression from exposed to infected, as it affects the speed of transitions between compartments.
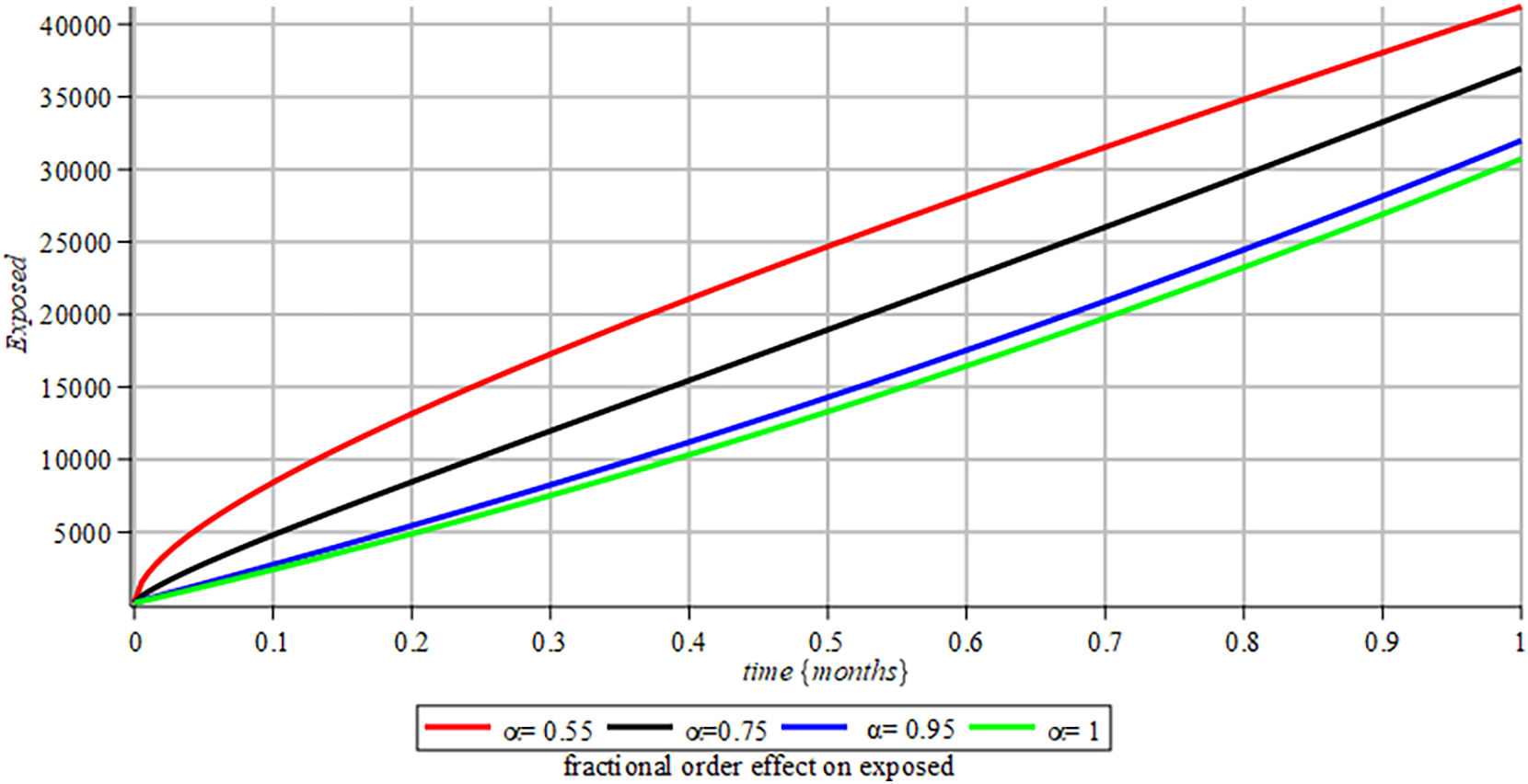
Figs. 7–12 evaluate the performance of the proposed fractional-order variation model in simulating the disease dynamics. When model parameters are modified, the model generates diverse results, offering flexibility in reproducing compartmental responses under various conditions. Figs. 9 and 11 emphasize the importance of large initial datasets for longer study intervals, as smaller initial populations may lead to implausible results, such as negative population sizes, during extended simulations.
Impact of Vaccination (Figs. 13 and 14):Fig. 13 shows that an effective vaccine significantly reduces the size of the susceptible population. In turn, Fig. 14 demonstrates how the vaccine indirectly lowers the likelihood of infection spread by reducing the number of exposed individuals. These findings underscore the importance of parameter-specific interventions in managing the dynamics of COVID-19.
The adaptability of the fractional-order model to different scenarios makes it a valuable tool for improving prediction accuracy. Furthermore, vaccination has a direct impact on the fundamental reproduction number, R, and remains a critical component in reducing both the susceptible and exposed populations. By simulating the spread of the disease and reducing contact rates among susceptible individuals, A consequence of the Omicron variant's appearance in our community is that it is feasible to contain the epidemic and boost vaccination effectiveness. it is imperative that we implement effective strategies to mitigate the outbreak.
ConclusionThis study employs a unique Caputo fractional-order mathematical model within the SEVIAR framework, incorporating vaccine efficacy, to explore SARS-CoV-2 variants using actual NCDC data from Rivers State, Nigeria. Determining the reproductive number is essential for understanding transmission rates, and the study integrates both qualitative and quantitative analyses. Sensitivity analysis examines the effects of parameters on various sub-compartments. The research emphasizes the usefulness of the LADM in infectious disease modeling, highlighting its ability to provide analytical solutions and guide preventive measures. Numerical simulations underscore the necessity of an alpha value of 1 for optimal reliability, while parameter assessments emphasize the importance of thorough validation. Visual representations illustrate the model's effectiveness in predicting outbreaks and evaluating intervention strategies.
Ultimately, this study enhances our understanding of infectious disease dynamics and provides valuable insights for proactive control measures against variants. Future work could expand the model and dataset to incorporate multi-regional or international data for broader applicability, as well as additional compartments or stochastic features to account for environmental and behavioral factors influencing transmission. Other considerations include waning immunity. Broadening the model to encompass new variants or diseases and developing interactive tools for policymakers would further enhance its utility in global epidemic control.
Ethics approval and consent to participateNot applicable.
Consent for publicationNot applicable.
Availability of data and materialNot applicable.
Competing interestsThe authors declare that they have no competing interests.
FundingNot Applicable.
Authors' contributionsAkeem O. Yunus: Formal analysis, Writing - original draft, Methodology, Writing - original draft, Writing - review & editing. Morufu O. Olayiwola: Investigation, Supervision, Writing - review & editing.
The authors hereby acknowledge with thanks everyone who has contributed to the success of this research work.